Mapping Algorithm using Graphs

Do you have a friend who has a great sense of direction who can remember all the routes once he visits them? I guess you might. This uncanny ability to make a mental map and finding the route avoiding all obstacles is something that not only plagues human but also robots. Here I have complied some methods that mathematics provides using graph theory to map the maps.

Basics

Lets take a map:

Where red circle is the start and green circle the end

Now lets add some obstacles(where is the fun without obstacles):

Make a grid:

Now it basically becomes:

each box grid is a node and a set of nodes is a graph.

Grass Fire algorithm

We start by numbering the end as 0 and then the nearest as 1 the 2nd nearest as 2 and so on till we reach the start node.

Now go back from the start subtracting 1 from it for each step if you have two options choose anyone.

Voila! you have successfully navigated but is it the most optmised?.No so let’s see Dijkstra algorithm

Dijkstra algorithm

Its starts out as a graph with nodes and distance between them defined then you go to the adjacent nodes and see the distance

We have gone through all the adjacent nodes of A now next we go to node B then we to end node E as 7+9=16 which is updated now let’s see to C, the node has shorter distance already so we don’t update We go to node C now the distance to D is updated as the shorter path to A through C so 3+1=4 same goes for node E. We again do the same on node D.

The Final path starts from A next goes to C then D then end E.

So we found the shortest path, so is this the best algorithm?? No this lags as all nodes have to be visited this makes this computationally intensive. So there is an algorithm which fixes this A* algorithm.

A* algorithm

A* algorithm is an addition to the Dijkstra where we attach a heuristic value to each node which is obtained using a heuristic function eg: .So in this the choice of which node will be first made on the value of the least distance. This is the A* algorithm where red nodes which it has visited and blue it needs to visit.

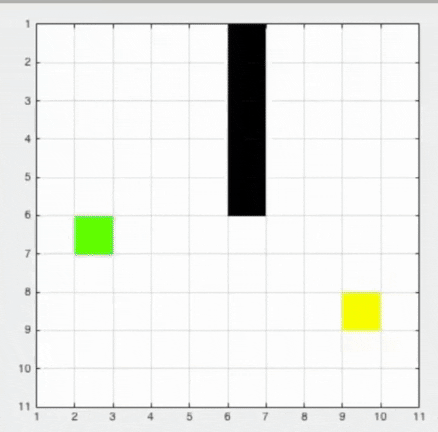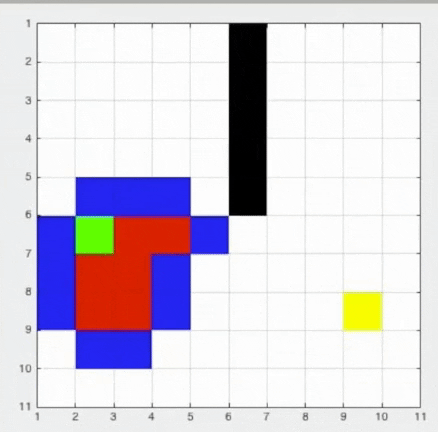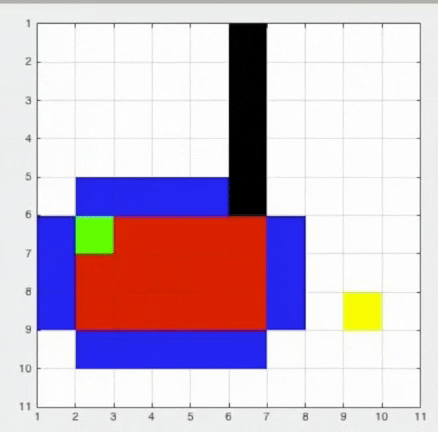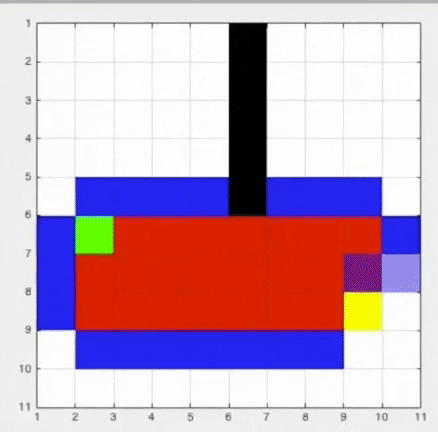See how it is targeted to the goal.

Now lets see Dijkstra:

See how spread out it is and how the heuristic function helped us direct our choices to the goal.

Conclusion

So now we know how Terminator found Sarah :P.